
视频课程
详细介绍
####
#####2.10二次函数
一般地,若两个变量x,y之间的对应关系可以表示成为常数且的形式,则称y是x的二次函数。
二次函数的图像
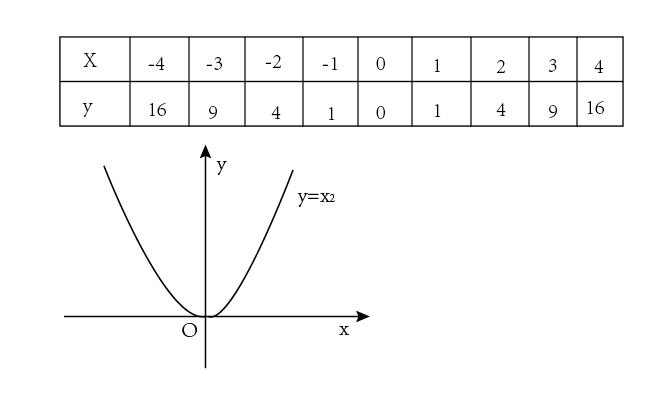
的图像特点
1.抛物线2.开口向上3.关于y轴对称4.抛物线的顶点:抛物线与对称轴的交点。
例:
若y=0,则x=-1或x=3
当x=1时,函数取最小值-4;
直线x=1是抛物线的对称轴;
x=-1或x=3是抛物线与x轴交点的横坐标。
的图像特点
若a>0,图像开口向上
若a<0,图像开口向下
当时,函数有最值
图像的对称轴为
C为与y轴交点的纵坐标
若C>0,抛物线与y轴的交点在原点上方
若C<0,抛物线与y轴的交点在原点下方
当时,函数取最值
即,抛物线的顶点坐标(,)
图像与x轴的交点有:2个,1个,0个
对应一元二次方程的的根:两个不相等的实数根,两个相等的实数根,无实数根
图像与x轴交点的横坐标就是一元二次方程的根
课程目录
暂无课程
资料下载
学习工具

都学单词

管综知识点

管综决胜800题

都学模考

政治刷题宝

MBA提面通

英文自我介绍一键生成

MBA院校库
用户评价
暂无用户评价
相关推荐

杨老师 

升学问题,微信私聊 ~
各大院校报考条件与流程、学费与学制,提前批政策、录取分数线,复试要求、招生数据,可以私聊咨询
返回顶部





